#proof-theory #philosophy-of-math #cognition

Can mathematical diagrams play an essential justificatory role in
mathematical proof? In a recent paper^[1], Silvia De Toffoli suggests
the affirmative, diverging from a commonly held view that diagrams play
at most a heuristic or illustrative role in mathematical
justification^[2]. She provides two important examples to demonstrate
that mathematical diagrams, subject to certain constraints, form genuine
notational systems: fundamental polygons in topology and commutative
diagrams in algebra. The basic argument is that, in either case, it is
possible to equip these diagrams with a syntax capable of supporting
logical inferences unambiguously corresponding to mathematical objects.
Furthermore, they satisfy desirable qualities of notation such as
reproducibility, stability, accessibility, and so on.

For example, consider the polygon diagram in Figure 1. The
constitutive features of this diagram -- labeled edges and vertices --
are Furthermore, it is straightforward (and, indeed, common practice)
for mathematical practitioners to reproduce these diagrams up to
non-constitutive features^[3]. Finally, practitioners can not only
perform (physical or mental) manipulations to these diagrams, but,
crucially, these manipulations correspond to well-defined mathematical
operations. In this case, together matching edges of a polygon
corresponds to forming a quotient space, and a polygon corresponds to a
homeomorphism of the surface. Therefore, polygon diagrams form a
notation system for topological surfaces that is not only intuitive^[4]
and natural for the topological setting, but also that supports
inferences with precise mathematical meaning.

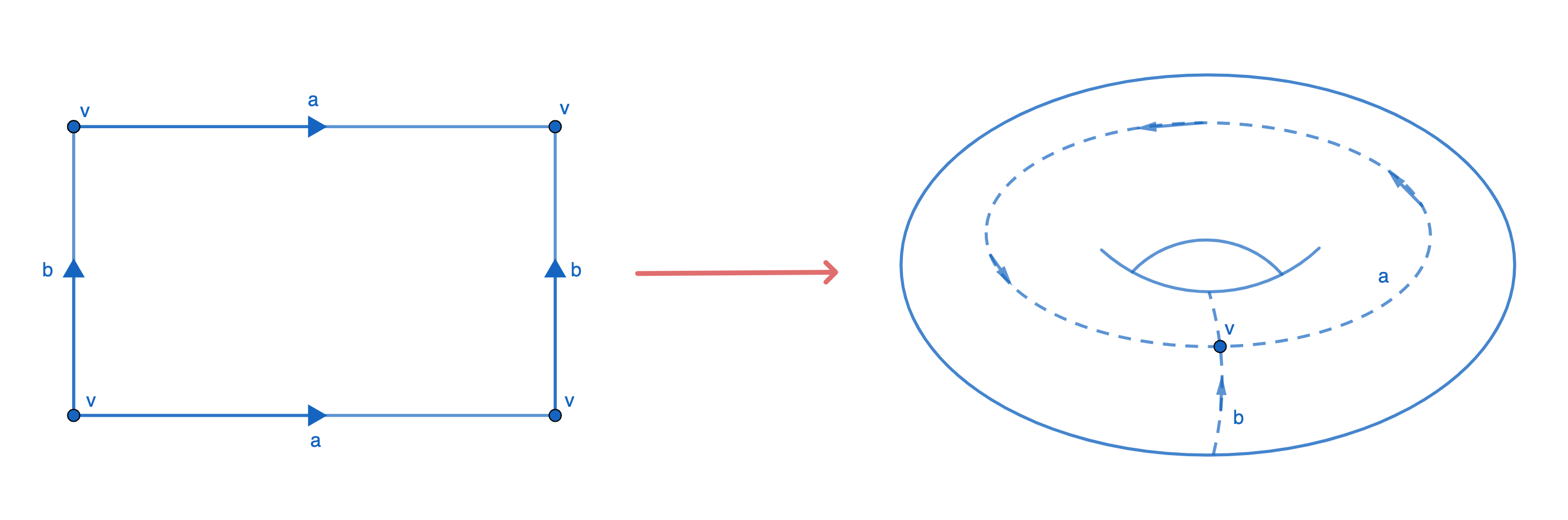
Figure 1. A polygon diagram and the corresponding torus

Examples like this settle the issue of whether diagrams can be used
for mathematical justification, in so far as they meet agreed upon
standards of rigor and criteria for acceptability^[5]; the natural
question, however, is whether there is actually epistemic merit to their
use in proofs, beyond the heuristic or illustrative value they might
provide. De Toffoli's second thesis addresses this explicitly: she
asserts the existence of a De Toffoli's justification for this claim
hinges on the nonexistence of a useful context-independent criterion for
proof identity. If one wishes to claim that two proofs of the same
proposition are he must specify a particular context of investigation.
Some examples of contexts are rigor -- two proofs of a proposition are
the same if they are equally rigorous -- and purity -- two proofs of a
proposition are the same if they use the same central idea.

The context of investigation relevant to De Toffoli's argument is that
of epistemic benefits and drawbacks, particularly as they relate to
cognitive efficiency and the practitioner's ability to grasp the overall
structure of a proof. In this setting, the primary differentiators
between proofs of the same proposition are factors contributing to
cognitive efficiency for a practitioner recreating or comprehending the
proof. De Toffoli's example of a proof involving diagrams lessening the
cognitive load on the practitioner is the snake lemma. This
fundamental result in homological algebra is somewhat tedious to prove
in prose alone, requiring the reader to bear in mind the properties of
several maps and the relationships between several abstract vector
spaces. Because of this, the result is almost always introduced, taught,
and remembered in terms of a commutative diagram -- indeed, the name
refers to the suggestive shape of the corresponding commutative diagram.
With the help of the diagram, the practitioner can both check each step
of the proof more reliably, as well as more easily grasp the global
structure of the problem. In this sense, the diagram bears much of the
cognitive burden that the practitioner carries when using the proof to
convince himself of the existence of a formal proof of the result.

The crux of De Toffoli's argument is that, in the context of epistemic
benefit, the discrepancy in cognitive efficiency of proofs of the
snake lemma with and without diagrams renders them different proofs of
the same proposition, even when they might be the same proof in the
contexts of rigor or purity. Therefore, the commutative diagram is an
essential feature of that proof in this context of investigation, and,
as such, the diagram cannot be faithfully into prose while retaining the
same proof. But how should qualities like explanatory power,
mathematical beauty, and purity fit affect the individuation of proofs
in the context of epistemic benefits, particularly in cases not
involving diagrams? This question casts doubt on whether this is even a
plausible conception of proof in the first place, or if this way of
individuating proofs might lead to undesirable results. This paper
serves as an introduction to the that De Toffoli mentions is necessary
to understand this phenomenon. In particular, I argue for a refined
understanding of proof individuation that retains the focus on epistemic
benefits and drawbacks as the primary individuator of proof
presentations, while balancing this with mathematical rigor and
mitigating undesirable judgments from subjective, agent-dependent
criteria.

In the following section, I will discuss whether epistemic benefit
actually yields a plausible, well-behaved identity criterion for proofs.
I will answer in the affirmative, with some key caveats. I will also
give a definition of an epistemic benefit, as well as a description of
the generic practitioner that might enjoy such benefits. There will be a
discussion of the commitments of engaging in this type of individuation,
with respect to mathematical rigor and acceptability. The final section
is a discussion of mathematical aesthetics and purity, which will
clarify the interplay between epistemic benefits/drawbacks and aesthetic
qualities often attributed to mathematical proofs.

Individuating Proofs

The set of all proof presentations surjects onto the set of provable
true propositions $P\to Q$. We can partition the set of proof
presentations by identifying any two presentations that are mapped by
this surjection to the same proposition. However, further refinement of
this partition requires a choice of a context of investigation; as De
Toffoli discusses, there is not a satisfactory context-independent
criterion for proof identity.^[6] However, there is concern as to
whether epistemic benefit is even a sensible condition for proof
identity in the first place as it relates to desirable features of
individuation, such as appropriate levels of specification,
subjectivity, universality, and so on.

But it is not immediately clear that the context of epistemic benefit is
well-behaved as a means to individuate proofs. For one -- when, if ever,
does this criterion actually equate proof presentations? In what sense
can actually be measured and/or effectively compared across proof
presentations? Furthermore, does this metric behave well with respect to
comparison across media types? That is, it is not clear a priori
whether it is even a coherent practice to compare diagrammatic and
non-diagrammatic proofs with respect to cognitive efficiency, in
general. Unless one can produce an example of a proof involving diagrams
and a proof not involving diagrams that are similar in terms of
epistemic benefits and drawbacks, the thesis that this proof criterion
renders diagrams essential to certain proofs is not reasonable.

The purpose of this section is to remedy some of these objections, as
well as to shed light on the motivation and meaning of some of the
underlying concepts. To begin with, we address the notion of cognitive
efficiency, as it relates to the epistemic benefits and drawbacks of a
proof. A boon for cognitive efficiency proffered by De Toffoli is if one
need not hold in mind a in order to see why steps are valid^[7]. This
benefit is clearly seen, for example, in the case of the snake lemma; as
many of the relevant maps and their relationships are semantically
embedded in a commutative diagram, the reader is free to grasp the
overall structure of the proof, while still being able to quickly refer
to the diagram to verify inferences. In this sense, the diagram
shoulders much of the cognitive burden of understanding a proof of the
snake lemma, therefore distinguishing it from a diagram-free version of
the proof, in which the diagrammatic moves have been faithfully encoded
in prose.

Importantly, mathematical diagrams whose roles are solely heuristic or
illustrative do not contribute to cognitive efficiency in the same
sense. According to De Toffoli's description, diagrams constitute
mathematical notation when they meet the following three criteria:

1. a notation should be cognitively accessible: its constitutive
   formal features should be clearly identified, persistent, and
   stable;

2. a notation should be reproducible: it should be possible for an
   average practitioner to copy its constitutive formal features with
   relative ease and reliability, possibly with the aid of different
   tools such as a straightedge and/or a computer;

3. a notation should support calculations and/or inferences: it
   should be possible for an average practitioner to perform
   reasonably simple manipulations corresponding to mathematical
   operations.

For a given proposition $P\to Q$, along with a proof presentation $A$
using diagrams that constitute mathematical notation and a proof
presentation $B$ using diagrams that do not constitute mathematical
notation, $A$ and $B$ differ as proofs with respect to the context of
epistemic benefits. To see this, we can evaluate the criteria in turn.
To begin with, suppose $B$ uses diagrams that are not cognitively
accessible. This clearly works against cognitive efficiency --
unraveling ambiguous, unstable diagrams imposes a highly nontrivial
cognitive load. Secondly, if the diagrams in $B$ are not easily and
reliably reproduced by a reader, then making manipulations or changes to
the diagrams corresponding to logical inferences can only be done in the
mind of the practitioner -- again, this arrests significant mental power
that would otherwise be left to grasping the large-scale structure of
the proof and making high level inferences. Finally, if the diagrams in
$B$ do not support logical inferences in the first place, then they
certainly provide no epistemic benefit with respect to justification.
None of these epistemic drawbacks, however, are imposed by
diagrams-as-notation. Thus, the secondary refinement of proof
presentations induced by epistemic benefit is fine enough to distinguish
between proofs like $A$ and proofs like $B$.

Subjectivity and agent-dependence

One might object that individuating proofs according to epistemic
benefit is not reasonable, due to possible discrepancies between
practitioners. I agree that it is necessary to mind possibly confounding
effects of being overly specific with respect to the cognitive strengths
and weaknesses of any one practitioner. However, it is still useful and
productive to make these judgments with an agent in mind; we need simply
to be careful about the precise role and nature of this agent. In order
to frame this issue more concretely, consider the following theorem.^[8]

Theorem 1. Whenever a rectangle is tiled by rectangles each of
which has at least one integer side, then the tiled rectangle has at
least one integer side.

This theorem^[9] was presented, along with a proof using a complex
double integral, at the 1985 Summer Meeting of the MAA, as a call to
attendees to find more simple or natural proofs of the theorem. This
call was successful: in the months that followed, several alternative
proofs of this theorem were presented, varying widely in simplicity,
techniques used, and strength (that is, the amount of generality in
which the proof may be applied). Two of these proofs are clear leaders
in terms of cognitive efficiency, though they employ strikingly distinct
techniques. Let $R$ be the specially tiled rectangle. Here I sketch
these two proofs.

1. Checkerboard. (R. Rochberg) Let $R$ be an $a\times b$ rectangle
   with a tiling by rectangles with at least one integer side, where
   $a$ and $b$ are real numbers. We may assume that $R$ is embedded in
   the plane with its lower-left corner at the origin. Then, consider
   the lattice obtained by tiling the plane by
   $\frac{1}{2}\times \frac{1}{2}$ black and white tiles, arranged in
   checkerboard fashion. Then, each of the tiles in $R$ contains an
   equal amount of black and white. Therefore $R$ contains an equal
   amount of black and white, as well.

   Now suppose for contradiction that neither $a$ nor $b$ is an
   integer. Then we may tile $R$ with four non-empty rectangles:
   $R_1=[0,\lfloor a\rfloor ]\times [0,\lfloor b\rfloor ]$,
   $R_2=[\lfloor a\rfloor ,a]\times [0,\lfloor b\rfloor ]$,
   $R_3=[0,\lfloor a\rfloor ]\times [\lfloor b\rfloor ,b]$,
   $R_4=[\lfloor a\rfloor ,a]\times [\lfloor b\rfloor ,b]$, as in Figure 2. Since each of $R_1,R_2$, and $R_3$
   have at least one integer side, they all contain equal amounts of
   black and white. However, $R_4$ does not contain equal amounts of
   black and white; this can be seen by an easy check using the facts
   that the sides of $R_4$ are all less than $1$ and that its lower
   left corner lies on a lattice point. Thus, the union
   $R=R_1\cup R_2\cup R_3\cup R_4$ does not contain an equal
   amount of black and white. This is a contradiction, so we may
   conclude that at least one of $a$ or $b$ is integral, as desired.
   $◼$

   
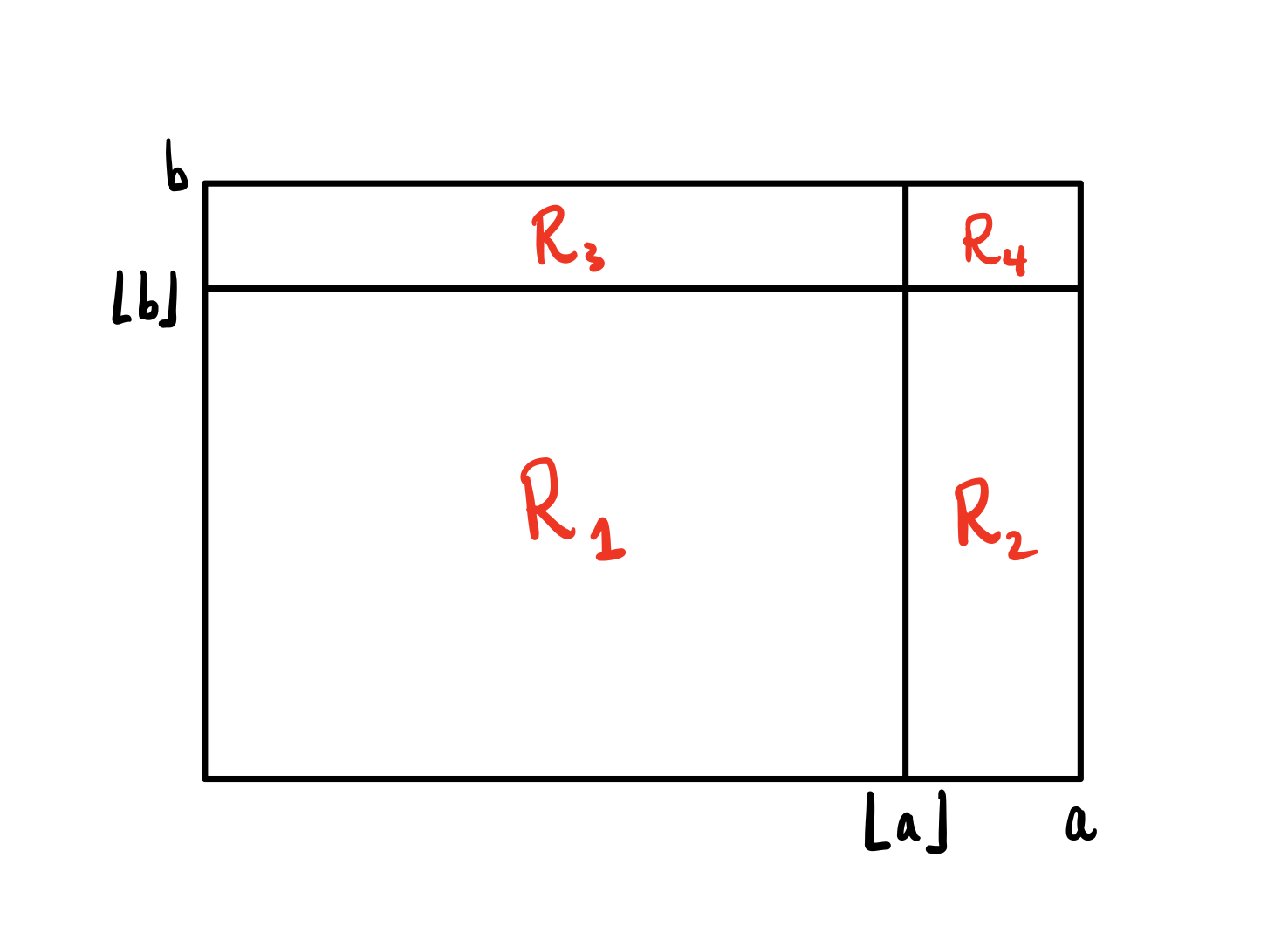
   Figure 2. Subdividing the rectangle R for Rochberg’s checkerboard proof.

2. Bipartite graph. (M. Paterson) Again embed $R$ in the plane with
   its lower left corner at the origin. Let $S$ be the vertex set of
   corners of tiles with both coordinates integral, and let $T$ be the
   set of tiles. We may form a bipartite graph $G$ on the union
   $S\cup T$ by connecting with an edge each point in $S$ with the
   elements in $T$ of which it is a corner, as in Figure 3.
   By the hypothesis, each element in $T$ has exactly $0$, $2$, or $4$
   corners in $S$. Therefore, $G$ has an even number of edges. Now,
   note that each element of $S$ which is not a corner of $R$ must lie
   on either $2$ or $4$ tiles -- hence it has even degree in $G$.

   But since the origin lies on only one element of $T$, there must be
   another point of $S$ lying on an odd number of tiles. Thus, there
   must be another corner of $R$ that lies in $S$. Therefore, either
   the width or the height of $R$ is an integer. $◼$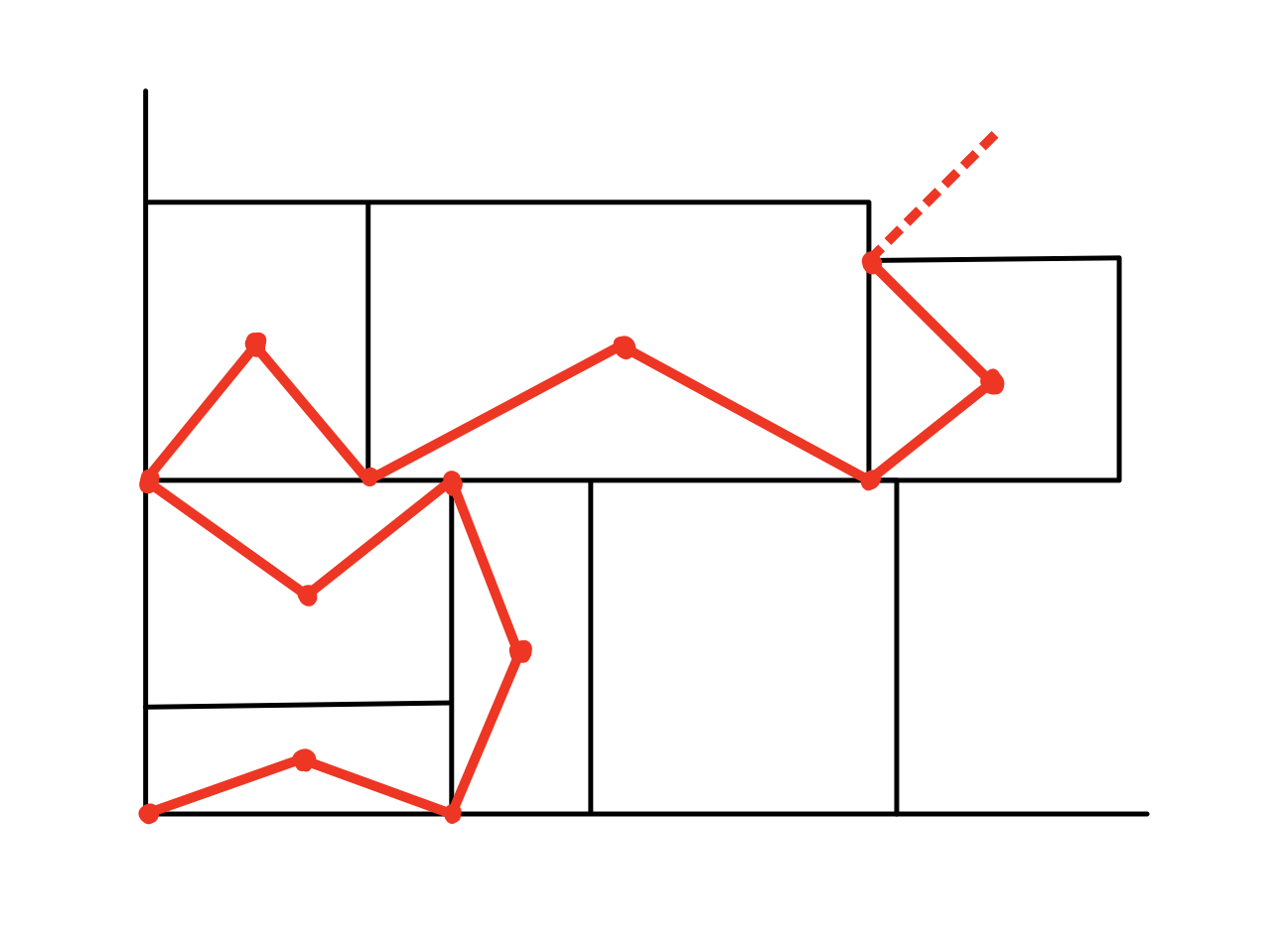

   
   Figure 3. A portion of the bipartite graph formed by a special tiling of a rectangle.

From the point of view of a particular practitioner, these two proofs
might present very different sets of epistemic benefits and drawbacks.
To begin with, for a student with no knowledge of basic graph theory,
the checkerboard proof is obviously more comprehensible. Therefore, with
Burgess' conception of rigor in mind, it makes sense to evaluate these
cognitive benefits in terms of a practitioner with sufficient background
in relevant areas of mathematics. Even then, a mathematician with
sufficient background for both proofs might feel a particular affinity,
hence be more likely to recall (an epistemic benefit), for one or the
other proof. For example, a graph theorist might be more drawn to the
bipartite graph proof; similarly, a mathematician with a preference for
constructive proof might prefer the bipartite graph proof.

Indeed, these proofs were posited by different mathematicians as being
the most proofs of the fact, even though they are so different with
respect to the techniques used; thus it is reasonable to assert that, to
the mathematician that formulated each proof, his own proof provided the
greatest epistemic benefit. Indeed, this is an ipso facto description
of mathematical practice: a mathematician proves propositions in the way
that makes the most sense to him. This principle contributes to an
account for the common mathematical practice of publishing new proofs of
previously established results. The rectangle-tiling theorem is a
particularly concrete example of this phenomenon, but this practice in
general speaks to the legitimacy of epistemic benefit (as well as
mathematical purity) as a quality that is valued by mathematicians, even
though it has no bearing on formal soundness.

To isolate what is happening here, it is helpful to actually name some
potential epistemic benefits and drawbacks of mathematical proof, and to
analyze them in the case of the two proofs of the rectangle tiling
theorem. De Toffoli mentions cognitive efficiency as a major epistemic
boon that is often bolstered by the inclusion of diagrams. Another
benefit is the ease with which a practitioner can verify the claims made
by the author of a proof. In this respect, the proofs of Theorem 1 have
a similar structure: after relevant definitions and setup are given,
each proof has one central inferential step which constitutes the crux
of the argument. In the former, it is the verification that $R_4$ does
not contain an equal amount of black and white; in the latter, it is the
verification that each of the interior points of $S$ have even degree in
$G$, and that the origin has odd degree in $G$. Interestingly, the way
in which one actually performs these verifications is also quite
similar. In each case, these claims are quickly checked by means of a
visualization of a general version of $R$, either in one's mind or drawn
on paper. Suggestive heuristic diagrams were provided in the original
versions of both proofs. In this sense, these proofs are similar with
respect to the epistemic benefit of ease of verification.

Another epistemic benefit might be the ease with which one can
communicate a proof in an informal setting -- this also contributes to
the ease with which a mathematician is able to recall and recreate a
proof. Once again, these two proofs of the tiling theorem are quite
similar in this respect. In presenting the checkerboard proof, one might
draw (on a chalkboard, for example) a sketch of a tiled rectangle, along
with a few suggestive squares of a checkerboard lattice. For the
bipartite graph proof, the same sketch might be drawn, supplemented
instead by a few edges of the bipartite graph, making sure to include
the odd degree vertex at the origin. This also sheds light on a
potential epistemic drawback shared by these two proofs: a dependence on
a certain level of spatial intuition from the reader.

This analysis makes clear two things: $(1)$ it is necessary to provide
an explicit characterization of what is meant by an epistemic benefit or
drawback. Here, we must tread carefully: if we are to redouble De
Toffoli's defense of the context of epistemic benefits and drawbacks
against Burgess' skepticism regarding heuristic or illustrative
diagrams, it is desirable that this conception of proof identity does
not distinguish along axes of explanatory power, methodological purity,
mathematical beauty, or other features of proof presentations relating
to mathematical aesthetics. If two proofs of $P\to Q$ differing only in
explanatory power are individuated in this context, De Toffoli's
argument meets a roadblock: then, a merely heuristic diagram (rather
than a diagram comprising honest-to-goodness mathematical notation)
could be considered essential to the identity of a proof.

And, $(2)$, this characterization should be made in reference to a
sufficiently generic mathematical practitioner; the cognitive benefit
offered by a proof might vary significantly depending on the background
and strengths of the reader.

In general, we may characterize an epistemic benefit as a feature of a
proof presentation that contributes to a generic practitioner's accurate
discovery, understanding, or communication of the proof. Similarly, an
epistemic drawback is a feature that detracts from a generic
practitioner's accurate discovery, understanding, or communication of
the proof. Here, is in reference to consistency with the established and
accepted body of mathematical knowledge. A generic practitioner is a
typical working mathematician with sufficient background to understand
and engage with the proof presentation in question.

Purity and Epistemic Benefit

De Toffoli describes the context of mathematical purity for
individuating proofs. Roughly, two proofs may be identified in this
setting if they use the same central idea. Furthermore, a proof of
$P\to Q$ may or may not exhibit : in David Hilbert's formulation,
whether it uses only the language, methods, and assumptions of that
which lies in the presentation of the proposition^[10]. But, in fact,
this feature of a proof can grant significant epistemic benefit.

Consider, for example, the development of the modern field of $p$-adic
Hodge theory. Inspired by the famous comparison theorem of de Rham,
which establishes an isomorphism between the de Rham cohomology and the
Betti cohomology of complex algebraic varieties, a deep and far-reaching
link between geometry and topology. The classical proof of this result
centers around an application of the Poincaré lemma, a statement about
the same differential forms used to define de Rham cohomology in the
first place.^[11]

This field was revived in the 1970s, when, spurred by developments in
algebraic geometry and Alexander Grothendieck's introduction of étale
cohomology, mathematicians sought to devise an analog of the de Rham
theorem for the étale cohomology of schemes over the $p$-adic numbers.
In 1988, Gerd Faltings proved Jean-Marc Fontaine's 1981 conjecture of
the existence of such an analogous isomorphism, but the structure of
Faltings' proof bore almost no resemblance to the classical
picture.^[12]

This field was revived in the 2010s when Alexander Beilinson, in order
to formulate a proof of Fontaine's conjecture using geometric
techniques, formulated a $p$-adic analogue of the Poincaré lemma that
enabled a proof of the existence of the $p$-adic comparison isomorphism
with the same overall structure as the classical proof. Beilinson's work
was remarkable for several reasons. To begin with, it presented
significant practical advantages for practitioners to understand and
communicate the proof; it is much easier to grasp the overall structure
of Beilinson's proof than Faltings', as the reader is able to compare it
at each step with the well-established classical proof of de Rham's
theorem. Indeed, the overarching structure of Beilinson's proof is
remarkably similar to the picture for complex varieties, as shown in. In each case,
the desired map $\rho$ factors through cleverly devised vector spaces,
enabled in each case by an application of the appropriate version of the
Poincaré lemma -- note the similarity of the corresponding commutative
diagrams. Though Beilinson's proof is not necessarily simpler or more
accessible than Faltings' in its own right, it succeeds in placing the
large-scale structure of the proof in a well-known existing mathematical
framework.^[13] This benefit demonstrates the epistemic power of
methodological purity and aesthetic alignment.

Beilinson's proof led to an era of fruitful mathematical discovery, on
the back of this new perspective in $p$-adic Hodge theory. The field of
$p$-adic Hodge theory was revived, leading to several years of fruitful
mathematical discovery using Beilinson's technique. Within the space of
a few years after the publication of Beilinson's proof, more progress
was made in the field than in the decade prior. Most notably, Bhargav
Bhatt enjoyed great success extending the $p$-adic Poincaré lemma to
much more general settings, and furthermore he adapted other classical
results in Hodge theory to the $p$-adic setting in Beilinson's simpler
framework, most notably the theory of spectral sequences.^[14]

Note that Beilinson's proof should be distinguished from Faltings' in
other respects as well. In the context of strength and generalizability,
for example, it is much more far-reaching; in the context of purity, it
is much more methodologically pure.^[15] The techniques used, the
definitions made, and the theory developed differ significantly for the
two proofs. Even still, they are also individuated purely on the basis
of epistemic benefit; this emphasizes the interplay between
distinguishing proofs in different contexts of investigation. There is a
case to be made that mathematical purity in most cases contributes
positively to epistemic benefit. De Toffoli hints at this in the case of
using polygon diagrams to prove statements about surfaces, mentioning
that It is thus reasonable to assert that using relevant diagrams as
such, in contributing to methodological purity, both contribute to
accurate understanding of a proof and to providing intuition about the
proof technique that can stimulate the discovery of related
propositions.

Here we must be careful. As mentioned before, it is not desirable for
the criterion of proof identity induced by epistemic benefits and
drawbacks to be so coarse as to allow merely heuristic mathematical
diagrams to distinguish proof presentations from their non-diagrammatic
counterparts. However, diagrams are a special case -- in the purview of
acceptability in mathematical practice,^[16] it is paramount that
diagrams meet some concrete standards for acceptability and mathematical
rigor, like those laid out by De Toffoli. On the other hand, for a proof
that does not contain notational diagrams as an essential component,
explanatory arguments, can in many cases (as in the Beilinson example)
contribute to accurate discovery, understanding, and communication in
their own right. In either case we are requiring that the epistemic
benefits are supported in a rigorous and mathematically acceptable way.

This discussion sheds light on the composite nature of proof identity,
and consequently the difficulty of formulating a satisfactory set of
criteria for individuating proofs. Though De Toffoli gave examples of
differentiating proofs based on epistemic benefit in the cases of proofs
containing notational diagrams, the aim of this section was to
understand how we might differentiate proofs along these lines in a more
general setting, in order to suggest that this way of individuating
proofs is well-behaved on a larger set of proof presentations.

Conclusion

Following De Toffoli's work justifying the essential role that certain
diagrams can play in the identity of mathematical proofs, we have
clarified the definition of epistemic benefits and drawbacks and
addressed the nature of the generic mathematical practitioner on which
this system relies. In short, an epistemic benefit (resp. drawback) is a
feature of a proof presentation that enhances (resp. hinders) the
discovery, understanding, and communication of the proof by a generic
practitioner. Epistemic benefits manifest, among other ways, as features
that reduce the cognitive load required to grasp, verify, or generalize
a proof. Some ways that they are realized in practice might be by use of
notational diagrams, as explored by De Toffoli, explanatory power,
methodological purity, or by placing an argument in an existing
mathematical framework.

The examples of the rectangle-tiling theorem and Beilinson's proof of
the comparison isomorphism demonstrate that we can distinguish along
lines of epistemic benefit in settings beyond proofs that contain
notational diagrams versus those that do not. This suggests that this is
a reasonable way to distinguish proofs in general, and indeed provides a
more general structure in which De Toffoli's contentions might fit. We
also addressed skepticism that might arise from the agent-dependence of
this practice. We also discussed why one must be careful when evaluating
epistemic benefits in the case of notational diagrams, as opposed to
usage of non-notational diagrams in proofs, in order to maintain
mathematical rigor and acceptability.

Additionally, we discussed the interplay between methodological purity,
rigor, and epistemic benefit, as well as the relationship of these
qualities with mathematical aesthetics. This is an area that merits more
exploration in future work.